히스토그램

1️⃣ 사전 지식

• 도수분포표: 자료를 일정한 계급으로 나누고 각 구간에 속하는 도수를 정리한 표야.
• 변량: 자료를 수량으로 나타낸 것이야.
• 계급: 변량을 일정한 간격으로 나누는 구간이야.
• 도수: 각 계급에 속하는 자료의 개수를 그 계급의 도수라고 해.

2️⃣ 핵심 개념

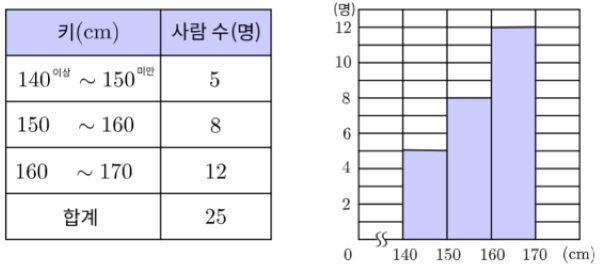
• 히스토그램은 도수분포표를 시각적으로 나타내는 그래프로, 구간별 도수를 막대 모양으로 표현해.

• 가로축은 각 계급을, 세로축은 각 구간에 속하는 자료의 도수를 나타내.

• 각 직사각형의 가로 길이는 계급의 크기와 같고, 높이는 도수와 같아.

• 히스토그램 만드는 방법

  1. 가로축에 각 계급의 끝 값을 적는다.
  2. 세로축에 도수를 적는다.
  3. 각 계급에서 계급의 크기를 가로로 나타내고 도수를 세로로 하는 직사각형을 그린다.

• 히스토그램의 중요한 특징은 직사각형의 넓이의 총합이 계급의 크기와 총 도수의 곱과 같다는 것이야.

• 직사각형의 넓이는 $\text{(계급의 크기)} \times \text{(그 계급의 도수)}$로 구해. 즉 각 계급의 도수와 정비례 한다는 것을 알 수 있지.

• 히스토그램은 자료의 분포를 한눈에 보여줘서 어떤 구간에 자료가 몰려 있는지 알 수 있어.

3️⃣ 예제 및 적용

• 학생들의 시험 점수를 $10$점씩 구간을 나누고 각 점수 구간에 속하는 학생 수를 히스토그램으로 그리면, 어떤 점수대에 학생이 많은지 알 수 있어.
• 하루 동안 시간대별 버스 승객 수를 $1$시간 간격으로 나누고 히스토그램으로 나타내면, 출퇴근 시간대에 승객이 많다는 것을 쉽게 확인할 수 있어.

4️⃣ 개념 정리

• 히스토그램은 도수분포표를 나타낸 것이라서 자료의 분포를 쉽게 볼 수 있어.
• 가로축은 구간, 세로축은 각 구간에 속하는 자료의 도수야.
• 자료가 어느 구간에 집중되어 있는지, 자료의 분포 모양을 알 수 있으니 자료 해석에 매우 유용해.
• 히스토그램을 잘 이해하려면 도수분포표와 구간 나누기를 먼저 확실히 익혀야 해.