부채꼴의 호의 길이와 넓이

1️⃣ 사전 지식

• 원의 중심각: 부채꼴에서 두 반지름이 이루는 각을 말해.
• 원의 반지름: 원의 중심에서 원 위의 한 점을 잇는 선분이야. 부채꼴은 두 반지름과 그 사이 호로 이루어진 도형이야.
• 원의 둘레의 길이: $\text{(원의 둘레의 길이)} = 2 \times \text{(반지름의 길이)} \times \text{(원주율)}$
• 원의 넓이: $\text{(원의 넓이)} = \text{(반지름의 길이)} \times \text{(반지름의 길이)} \times \text{(원주율)}$

2️⃣ 핵심 개념

• 원주율: 원의 크기와 관계없이 원주를 원의 지름으로 나눈, 항상 일정한 값을 말해. $3.141592653\cdots$과 같이 끊임없이 계속되는 소수로 알려져 있어. $\pi$와 같이 나타내고 파이라고 읽어.
• 반지름의 길이가 $r$인 둘레의 길이 $l$과 넓이 $S$를 $\pi$를 사용하여 나타내면 다음과 같아.
  $$l = 2\pi r, S = \pi r^2$$

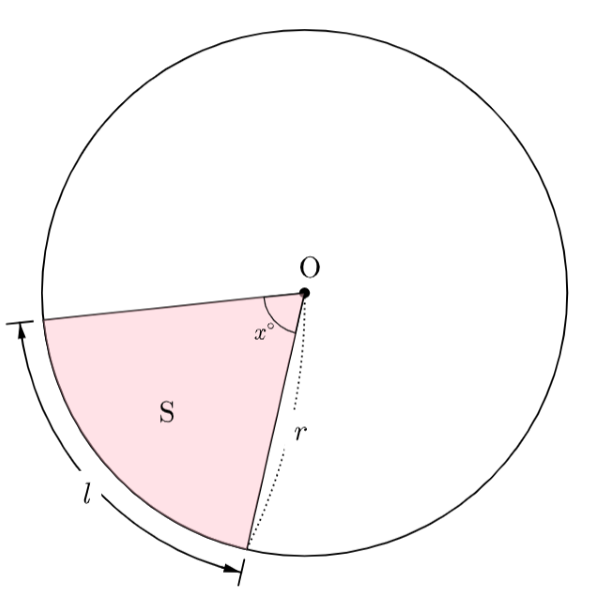
• 반지름의 길이가 $r$이고 중심각의 크기가 $x^\circ$인 부채꼴의 호의 길이 $l$과 넓이 $S$는 각각 중심각의 크기에 비례해. 즉,
  $$2 \pi r : l = 360 : x \text{ 에서 } l = 2\pi r \times \frac{x}{360}$$
  $$\pi r^2 : S = 360 : x \text{ 에서 } S = \pi r^2 \times \frac{x}{360}$$
  이야.
  • 예를들어 반지름의 길이가 $10\text{cm}$이고 중심각의 크기가 $60^\circ$인 부채꼴의 호의 길이$l$과 넓이$S$는 다음과 같아.
  • $l = 2\pi \times 10 \times \dfrac{60}{360} = \dfrac{10}{3}\pi$
  • $S = \pi \times (10)^2 \times \dfrac{60}{360} = \dfrac{100}{6} \pi$
• 부채꼴의 넓이는 반지름의 길이와 호의 길이를 이용하여 구할 수도 있어.
  • $S = \pi r^2 \times \dfrac{x}{360} = \dfrac{1}{2} \times r \times (2\pi r \times \dfrac{x}{360}) = \dfrac{1}{2}rl$
• 따라서 중심각의 크기를 구하지 않아도
  $$S = \frac{1}{2}rl$$
  으로 구할 수 있어.

3️⃣ 예제 및 적용

반지름이 $5 \ \text{cm}$이고 중심각이 $90^\circ$인 부채꼴의 호의 길이와 넓이를 구하면,
$$l = 2 \pi \times 5 \times \frac{90}{360} = \frac{5}{2}\pi \, (\text{cm}) \hspace{0.4cm}$$
$$S = \pi \times 5^2 \times \frac{90}{360} \hspace{2.12cm}$$
$$= \frac{1}{2} \times 5 \times \frac{5}{2}\pi = \frac{25}{4}\pi \,(\text{cm}^2)$$

4️⃣ 개념 정리

• 부채꼴의 호의 길이는 원의 둘레에서 중심각에 해당하는 부분의 길이야.
• 부채꼴의 넓이는 원의 넓이에서 중심각에 해당하는 부분의 넓이야.
• 두 값은 모두 중심각과 반지름에 비례하며, 호의 길이가 길어질수록 넓이도 커져.
• 중심각을 바꾸거나 반지름을 바꾸면 부채꼴의 크기가 어떻게 변하는지 직접 계산해 보는 게 이해에 도움돼.