중심각의 크기와 호의 길이, 넓이, 현의 길이 사이의 관계
'중심각의 크기와 호의 길이, 넓이, 현의 길이 사이의 관계'의 개념을 설명해줘
1️⃣ 사전 지식
- 원의 중심과 반지름: 원은 중심에서 같은 거리에 있는 점들이 이루는 도형이야. 중심에서 원 위의 한 점까지의 거리를 반지름이라고 해.
- 호: 원 위의 두 점을 연결하는 원의 일부야.
- 중심각: 원의 중심에서 원 위의 두 점을 잇는 두 반지름이 만드는 각이야.
- 부채꼴: 호와 그 호의 끝 점과 원의 중심을 이은 두 반지름이 이루는 도형을 말해.
2️⃣ 핵심 개념
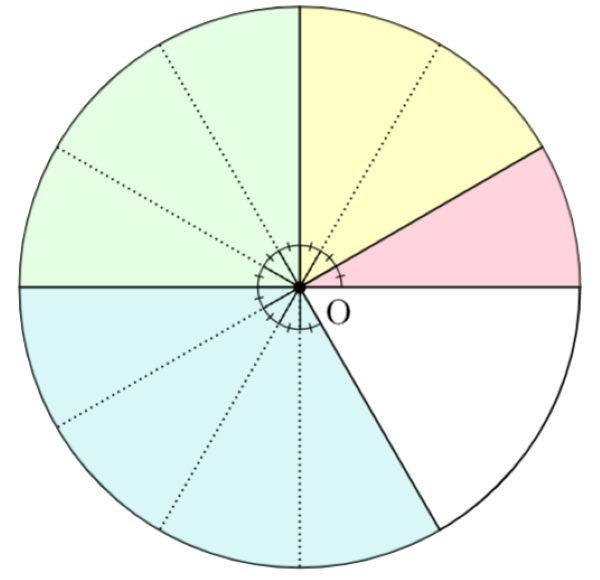
- 중심각의 크기와 호의 길이의 관계: 한 원에서 부채꼴의 중심각의 크기가 배, 배, 배, ...가 됨에 따라 부채꼴의 호의 길이도 배, 배, 배, ...가 돼. 즉, 한 원에서 부채꼴의 호의 길이는 부채꼴의 중심각의 크기에 정비례해.
- 중심각의 크기와 부채꼴의 넓이 관계: 한 원에서 부채꼴의 넓이도 부채꼴의 중심각의 크기에 따라 달라져. 부채꼴의 중심각의 크기가 배, 배, 배, ...가 됨에 따라 부채꼴의 넓이도 배, 배, 배, ...가 돼. 즉, 부채꼴의 넓이 역시 부채꼴의 중심각의 크기에 정비례해.
- 한 원에서 중심각의 크기가 같은 두 부채꼴의 호의 길이와 넓이는 각각 같다는 것도 알 수 있어. 이는 반지름이 같은 두 원에서도 해당돼.
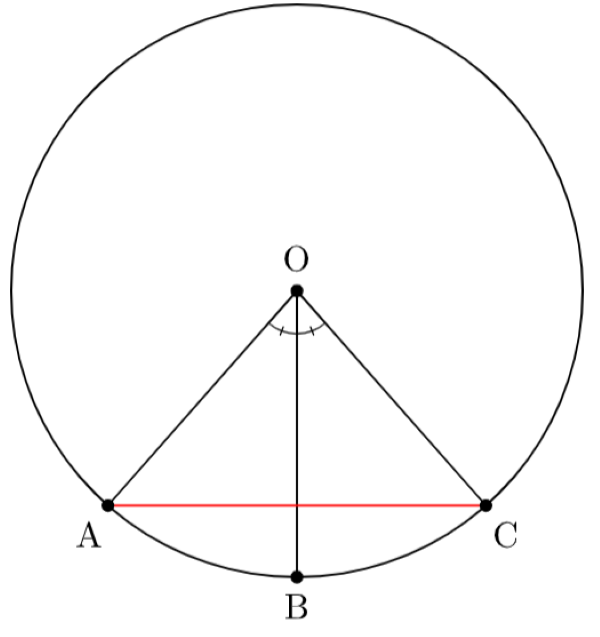
- 한 원에서 중심각의 크기가 같은 두 현의 길이는 같아.
- 부채꼴 와 부채꼴 는 중심각의 크기가 같으므로 야.
- 한 원에서 현의 길이는 중심각의 크기에 정비례하지 않아.
- 현의 길이가 중심각의 크기에 정비례한다면 이어야 해.
- 그런데 에서 야. 따라서 이 성립하지 않으므로 현의 길이와 중심각의 크기는 정비례하지 않음을 알 수 있어.
3️⃣ 예제 및 적용
- 피자를 일정한 크기로 나눌 때, 각 조각의 중심각이 클수록 피자 조각의 테두리(호의 길이)가 길어지고, 조각의 넓이도 커져. 그래서 더 큰 조각을 원하면 중심각을 크게 만들어야 해.
- 반지름이 인 원에서 중심각이 인 부채꼴과 도인 부채꼴을 생각해 보자. 중심각이 두 배가 되면 호의 길이와 넓이도 두 배가 된다는 사실을 알 수 있어.
4️⃣ 개념 정리
- 한 원에서 중심각의 크기가 같은 두 부채꼴의 호의 길이와 넓이는 각각 같아.
- 한 원에서 부채꼴의 호의 길이와 넓이는 각각 부채꼴의 중심각의 크기에 정비례해.
- 중심각, 호, 부채꼴을 구분하고 이들 사이의 관계를 머릿속에 잘 정리해 두는 게 중요해!
중심각이 두 배가 되면 부채꼴의 넓이도 항상 두 배일까?
실생활에서 중심각과 호의 길이 관계를 이용하는 경우는 무엇이 있을까?
시계 초침이 움직이는 호의 길이는 중심각과 어떤 관계일까?
이어서 질문하기
'개념(익히기)' 풀기 Enter
'중심각의 크기와 호의 길이, 넓이, 현의 길이 사이의 관계'의 특성에 대해 조금 더 자세히 설명해줘
중심각이 두 배가 되면 부채꼴의 넓이도 항상 두 배일까?
실생활에서 중심각과 호의 길이 관계를 이용하는 경우는 무엇이 있을까?
시계 초침이 움직이는 호의 길이는 중심각과 어떤 관계일까?
(2) 중심각의 크기와 호의 길이, 부채꼴의 넓이 사이의 관계 [04 원과 부채꼴] 중1-2학기 개념수학
(3) 중심각의 크기와 현의 길이 사이의 관계 [04 원과 부채꼴] 중1-2학기 개념수학
[EBS 수학의 답] 원과 부채꼴 - 중심각의 크기와 현의 길이
