길이가 같은 선분의 작도, 크기가 같은 각의 작도

1️⃣ 사전 지식

• 점: 위치를 나타내는 도형으로, 크기나 넓이가 없어.
• 선분: 두 점을 연결한 곧은 선으로, 시작점과 끝점이 있어.
• 각($\angle$): 한 점에서 시작하는 두 반직선으로 이루어진 도형이야.
• 교점: 선과 선, 또는 선과 면이 만나서 생기는 점을 말해.
• 작도: 눈금 없는 자와 컴퍼스만 사용해서 도형을 그리는 방법을 말해.

2️⃣ 핵심 개념

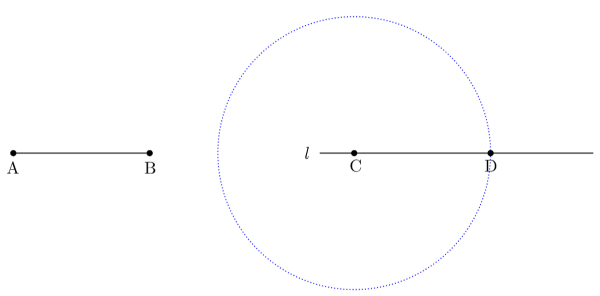
• 길이가 같은 선분의 작도는 이미 있는 선분 $\text{AB}$와 똑같은 길이의 선분 $\text{CD}$를 자와 컴퍼스만으로 그리는 거야. 그리는 방법은 다음과 같아.
  1. 눈금 없는 자를 이용하여 직선 $l$을 그리고 그 위에 점 $\text{C}$를 찍는다.
  2. 선분 $\text{AB}$의 길이를 컴퍼스로 잰다.
  3. 점 $\text{C}$를 중심으로 반지름이 선분 $\text{AB}$의 길이인 원을 그린다.
  4. 직선 $l$과 교점인 부분을 $\text{D}$라고 하면 $\overline{\text{AB}}$와 길이가 같은 선분 $\text{CD}$를 그릴 수 있다.

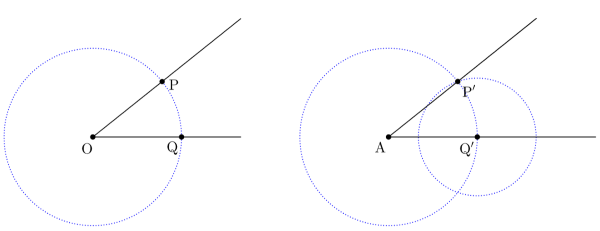
• 크기가 같은 각의 작도는 주어진 각 $\angle \text{O}$와 크기가 똑같은 각 $\angle \text{A}$를 자와 컴퍼스만으로 만드는 거야. 그리는 방법은 다음과 같아.
  1. 점 $\text{O}$를 중심으로 하는 원을 그려 $\angle \text{O}$의 두 변과의 교점을 $\text{P}$, $\text{Q}$라고 한다.
  2. 점 $\text{A}$을 중심으로 반지름 길이가 $\overline{\text{OQ}}$인 원을 그려주고, 반직선과 교점인 부분을 $\text{Q}'$이라고 한다.
  3. 컴퍼스를 사용하여 $\overline{\text{PQ}}$의 길이를 잰다.
  4. 점 $\text{Q}'$을 중심으로 반지름 길이가 $\overline{\text{PQ}}$인 원을 그린 후, 위에서 그린 원과의 교점을 $\text{P}'$이라고 한다.
  5. $\overrightarrow{\text{AP}'}$을 그어주면 $\angle \text{O}$와 크기가 같은 $\angle \text{A}$를 그릴 수 있다.

3️⃣ 예제 및 적용

• 길이가 같은 선분의 작도: 목공이 나무 조각을 똑같은 길이로 자를 때 사용해.
• 크기가 같은 각의 작도: 건축 현장에서 같은 각도로 부품을 맞출 때, 활용돼.

4️⃣ 개념 정리

• 길이가 같은 선분의 작도는 눈금 없는 자와 컴퍼스를 이용해 주어진 선분의 길이를 옮겨 그리는 거야.
• 크기가 같은 각의 작도는 눈금 없는 자와 컴퍼스로 크기가 같은 각을 옮겨 그리는 거야.
• 연습할수록 손에 익고, 도형 문제에 큰 도움이 돼! 😊