이등변삼각형이 되는 조건
'이등변삼각형이 되는 조건'의 개념을 설명해줘
1️⃣ 핵심 개념
- 이등변삼각형은 두 변의 길이가 같은 삼각형을 말해.
- 두 내각의 크기가 같은 삼각형은 이등변삼각형이 된다고 할 수 있어.
- 즉, 만약 라면, 두 변 와 의 길이가 같아.
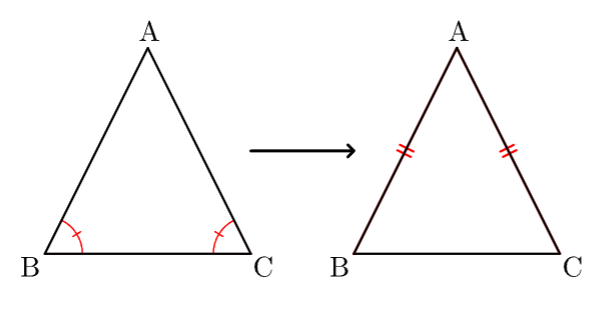
2️⃣ 개념 더 알아보기
이런 관계는 삼각형의 합동 조건 중 하나인 합동(각-변-각)으로 증명할 수 있어.
대응하는 한 변의 길이가 같고, 그 양 끝 각의 크기가 각각 같은 두 삼각형을 합동이라고 해.
인 에서 의 이등분선과 변 의 교점을 점라고 가정해 보자.
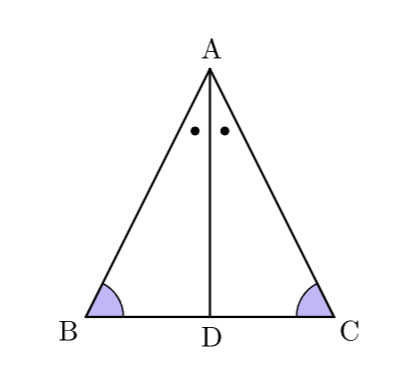
와 에서
에 의하여 (합동)이므로 임을 알 수 있어.이것이 바로 두 내각의 크기가 같은 삼각형은 이등변삼각형 증명이고, 이 조건이 이등변삼각형이 되는 조건이야.
3️⃣ 예제 살펴보기
삼각형 에서 이고 라고 하자.
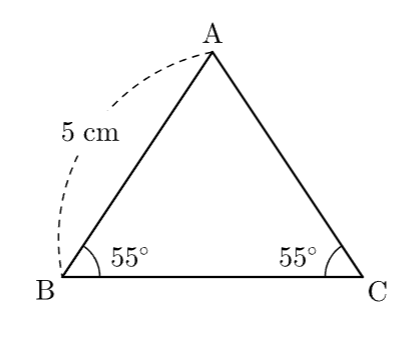
두 각이 같으니, 두 변 와 도 같아져야 해.
만약 라면, 가 되는 거야.
이때, 삼각형 는 두 변의 길이가 같으므로 이등변삼각형이야.
이렇게 각의 크기를 알면 변의 길이가 같다는 사실을 알 수 있고, 삼각형의 모양도 쉽게 파악할 수 있어.
이등변삼각형에서 두 각이 같은 이유는 무엇일까?
일상에서 이등변삼각형 모양을 볼 수 있는 예는 무엇일까?
두 각이 같지 않으면 이등변삼각형이 될 수 없을까?
이어서 질문하기
'개념(익히기)' 풀기 Enter
'이등변삼각형이 되는 조건'의 특성에 대해 조금 더 자세히 설명해줘
이등변삼각형에서 두 각이 같은 이유는 무엇일까?
일상에서 이등변삼각형 모양을 볼 수 있는 예는 무엇일까?
두 각이 같지 않으면 이등변삼각형이 될 수 없을까?
[EBS 수학의 답] 이등변삼각형과 직각삼각형 - 이등변삼각형이 되는 조건
